Exploring the mathematics of origami has been a pursuit of recreational mathematicians, educators, and mathematical researchers for some time. Martin Gardner's chapter on the mathematics of origami in The Second Book of Mathematical Puzzles and Diversions remains a good starting point for anyone who is curious. Barry Cipra's article in the October 2001 SIAM News is more recent survey that stresses the applications of the mathematical approach to origami (for more applications see Simon Guest on 'deployable structures').
Exploring the mathematics of origami has been a pursuit of recreational mathematicians, educators, and mathematical researchers for some time. Martin Gardner's chapter on the mathematics of origami in The Second Book of Mathematical Puzzles and Diversions remains a good starting point for anyone who is curious. Barry Cipra's article in the October 2001 SIAM News is more recent survey that stresses the applications of the mathematical approach to origami (for more applications see Simon Guest on 'deployable structures').Three mathematicians that are at the forefront of the research end of this topic are Robert Lang, Erik Demaine, and Tom Hull. All three are featured in the Institute for Figuring's online exhibit "Mathematical Paper Folding." Erik Demaine has a downloadable book chapter that provides a nice overview of recent advances in the subject. Robert Lang's paper with Roger C. Alperin outlines some of the axiomatic approaches to the mathematics of origami. There are some down loadable worksheets from Tom Hull's book, Project Origami, here.
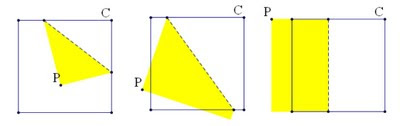
One set of activities in Hull's book introduces Kazuo Haga's "origamics," which is an approach to teaching the mathematics of origami that emphasizes experimentation and discovery. One of explorations asks students to look at making a single fold and observing what polygon is created by the "turned up part" (do you get a triangle, square, or other polygon? when and why do different polygons occur?). The appeal of this activity is its simplicity, a simplicity that also allows it to be modeled effectively in Geometer's Sketchpad (a GSP file for this activity is here, and solutions here).
In addition to the activities in this book (and many others), there are some great videos available that show how origami can be integrated into mathematics education. A webinar for Ontario teachers is archived here, and an inspiring overview of an Israeli program ('Origametria') is shown here. Using origami in education is not new - in the West it was introduced by Friedrich Fröbel along with the concept of kindergarten (see another TIFF online exhibit, Inventing Kindergarten). The history of teaching with origami in Japan, of course, goes back further still.
Despite its history, this is definitely a very current subject: the documentary film Between the Folds is on the film festival and conference circuit right now, and is apparently going to be generally available for purchase in the fall.
Beautiful mathematics is only part of the appeal of origami - the stunning transformations that can be achieved through origami are what really attract people to it - witness Sara Adam's miraculous construction of the Robert Lang cuckoo clock.