Illustration by John Tenniel
Here is another logic puzzle by Raymond Smullyan, this time from his book Alice in Puzzle-Land:
Just then Alice practically stumbled on Tweedledum and
Tweedledee, who were grinning under a tree right by their house.
Alice looked carefully at their collars to see which was marked
"Dum" and which was marked "Dee," but neither collar was
embroidered.
"I'm afraid I can't very well tell you apart without your embroidered
collars," remarked Alice.
"You'll have to use logic," said one of the brothers, giving the
other an affectionate hug. "We were expecting you to come around
these parts, and we have prepared some nice logic games for you.
Would you like to play?"
"As you see, this is a red card. Now, a red card signifies that the
one carrying it is telling the truth, whereas a black card signifies that
the speaker is telling a lie. Now, my brother there [he pointed to the
other one] is also carrying either a red card or a black card in his
pocket. He is about to make a statement. If his card is red, he will
make a true statement, but if his card is black, he will make a false
statement. Then your job is to figure out whether he is Tweedledee
or Tweedledum."
"Oh, that sounds like fun!" said Alice. "I'd like to play!"
...Well, Tweedledee [and Tweedledum] went into the house, and both
brothers came out shortly after. They look more alike than ever! thought
Alice. Well, one of them—call him the first one—stood to Alice's left,
and the other—call him the second one—stood to Alice's right. They
then made the following statements:
FIRST ONE: My brother is Tweedledee, and he is carrying a black card.
SECOND ONE: My brother is Tweedledum, and he is carrying a red card.
Which one is which?
If you think you may have a solution, you can try it out against the online version here.
After solving a puzzle (or reading the solution) in one of Smullyan's books, I am often left wishing there were more like it. Why not try generating some more?
Let's say there are 8 simple statements each brother could make.
- My name is [Tweedledee|Tweedledum].
- I am carrying a [red|black] card.
- My brother's name is [Tweedledee|Tweedledum].
- My brother is carrying a [red|black] card.
- My name is [Tweedledee|Tweedledum] [and|or] I am carrying a [red|black] card.
- My brother's name is [Tweedledee|Tweedledum] [and|or] he is carrying a [red|black] card.
But some of these puzzles will lead to contradictions. For example, if either brother makes the statement "I am carrying a black card." We end up with the liars paradox: the brother must be lying, but if he is, he is telling the truth (and vice versa). Some of these also lead to multiple solutions.
A good puzzle must have a unique solution, and running these through a logic-puzzle solver yields 168 good puzzles (you can check out a Python notebook that generates and verifies the puzzles here). Really, only half of these puzzles are unique, as having the anonymous brothers "first one" and "second one" switch statements gives us essentially the same puzzle. So, ignoring the order of the statements/brothers there are 168/2 = 84 unique puzzles based on these statements.
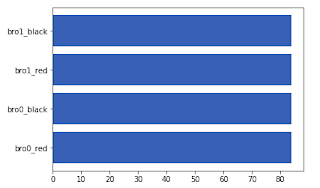
The distribution of names and cards is uniform in these 84 puzzles (the brothers are as likely to be telling the truth as they are to be lying). In the graphs below the brothers are referred to as bro0 and bro1, and the counts are based on the set of 168 puzzles where the 'reverse' of each puzzle is also included.
cards held by both brothers
cards held by each brother