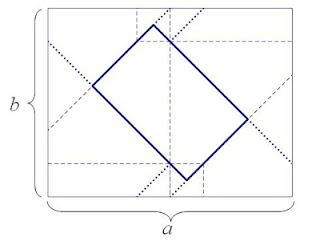
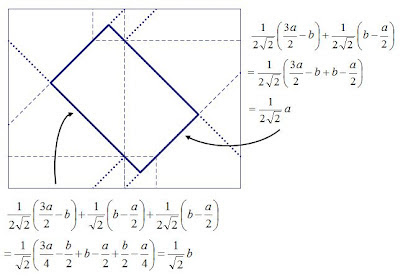
A while ago, I posted an exploration of the origami envelope featured on Origami USA's free diagram page that showed that the central rectangle formed in the crease pattern that contributes to the front (or back) of the completed envelope is 1/4 the area of the original paper (see here for that).
Jose Ignacio Royo Prieto (http://www.ehu.eus/joseroyo/), a mathematician with an interest in origami, recently provided me with a much nicer argument that allows you to directly see this area relationship while folding or holding the envelope in your hands. As Jose explains:
I very much prefer to argue by counting the layers of the final model: there are four of them in every point of the envelope (this homogeneity is remarkable), save in the two pocket-triangles, containing six layers. But the pocket-triangles are double the size of the missing triangles necessary to get the rectangle, so it is four layers in the whole small rectangle.
This provides a tangible and intuitive way to understand the area relationships in the model, and a nice example of an origami-centered way of thinking mathematically.
When Jose explained this to me, I was reminded of some recent stories about how prevalent and important folded envelopes and paper letter locks were in the past, and wondered where origami envelopes might fit into the periodic table of letter locks, described here: http://letterlocking.org/categories (only the F, and F+T rows, I think). Here again, Jose provided some helpful guidance:
Well, there is some controversy. The most spread consensus is the following, in my opinion: an envelope must look like an envelope and have a flap that, in the final move, closes/locks everything. Other folds not having this feature, but that have locks, are just called letterfolds. An envelope is suitable and, in fact, designed to contain other things. The letterfold is a clever/nice way to fold a letter after being written. Long as it is, this explanation does not close the debate, I think!
The envelope (and letterfold) featured on Origami USA's diagram page is a really nice one, but there are others that Jose recommends: Swamy's letterfolds (particularly this one), and the models found on Paula's Orihouse (particularly Paul Jackson's "tres bon" model).