I shall just sit down for a moment and pop on my boots and then I'll be on my way.
Speaking of ways, pet, by the way, there is such a thing as a tesseract.
Mrs. Murry went very white and with one hand reached backward and clutched
her chair for support. Her voice trembled. "What did you say?"
- A Wrinkle In Time, Madeleine L'Engle
Speaking of ways, pet, by the way, there is such a thing as a tesseract.
Mrs. Murry went very white and with one hand reached backward and clutched
her chair for support. Her voice trembled. "What did you say?"
- A Wrinkle In Time, Madeleine L'Engle
We're likely not as troubled by tesseracts as Mrs Murry, but it is a nice little surprise when you come across them when they're unlooked for. You'll encounter them (or at least their 1-skeletons, the vertices and edges) while drawing factor lattices.
A factor lattice for a number n has as its nodes all factors of n. Two nodes a and b have an arrow (directed edge) between them if a divides b. Usually we don't draw all the arrows, just the ones where b/a is a prime factor of n - all the other arrows are found by composition, or are the trivial arrows that are the loops on each node (a divides a). (In this way, factor lattices are nice examples of very simple and special categories). Some notes on drawing factor lattices are here.
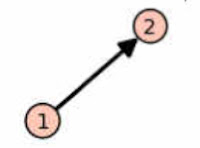
The factor lattice for 1 is just a single node.
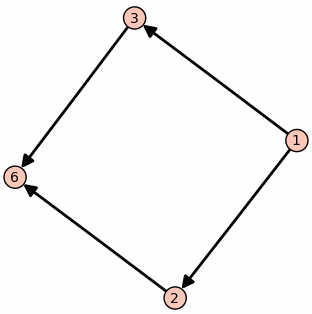
A number like 6, that is the product of two primes gives a factor lattice that looks like a square.
A number like 30 that is the product of three distinct primes produces a factor lattice that looks like a cube.
And 210 is, you guessed it, the smallest number that produces a factor-lattice that looks like a (squished frame of a) tesseract (the 4-dimensional hypercube).
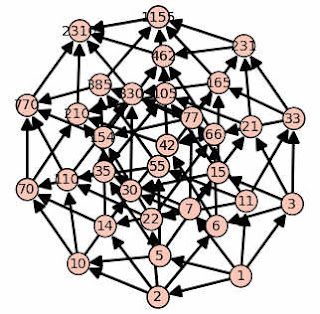
You can go further (of course) but it gets harder to see what's going on in the diagrams. 2310 is the smallest number that gives us a 5-cube.