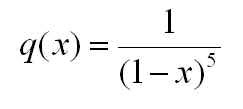The scrambler amusement park ride gives a visceral sense for how circular motions can be added together to create a trajectory that scarecely resembles a circle itself. If you watch (or get on) the ride, you'll see (or feel) that while the ride consists of a circular structure spinning on a larger spinning circle, riders seem to move in triangular or square paths (it was moving too fast for me to tell which).
The scrambler amusement park ride gives a visceral sense for how circular motions can be added together to create a trajectory that scarecely resembles a circle itself. If you watch (or get on) the ride, you'll see (or feel) that while the ride consists of a circular structure spinning on a larger spinning circle, riders seem to move in triangular or square paths (it was moving too fast for me to tell which).
When I tried to model the scrambler in Geometer's Sketchpad to learn more about the path that its riders follow, I chose to have point A traveling in one direction on a large circle, while point B travelled in the opposite direction on a circle whose radius was half the size of the first, centered on A. Both points were set to travel at the same speed. This gave a path very much like the scrambler's - a curved triangle.
 Different choices for the relative sizes and speeds of the circles and points give different curves. In this case, having the circles move in opposite directions creates a curve that is the simplest hypocycloid, while having the circles move in the same direction creates the simplest epicycloid.
Different choices for the relative sizes and speeds of the circles and points give different curves. In this case, having the circles move in opposite directions creates a curve that is the simplest hypocycloid, while having the circles move in the same direction creates the simplest epicycloid.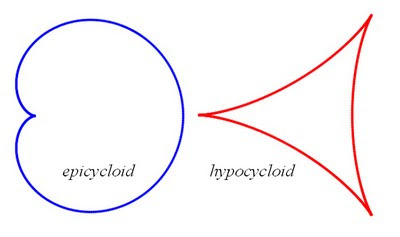
Hypocycloids are usually defined by having the small circle roll along the inside of the larger circle, while epicycloids are defined by having the small circle roll along the outside. By choosing the right rotation speed and sizes, you can get the same curves by having the small circle centered on the circumferences of the large circle, as I did when modeling the scrambler.
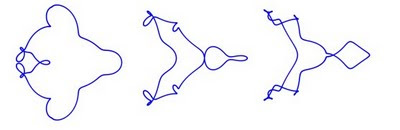
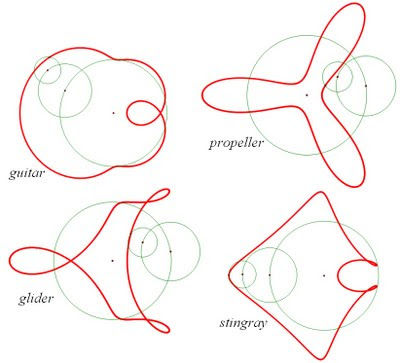
There are lots of ways to explore this model further, but one that appealed to me was to try to add additional circles spinning on top of the existing ones, with each additional circle having half the radius of the one it sits on. Having the circles spin in different directions generates very different curves (a further restriction was to start all circular motion in phase with all the points initially lined up). By varying the spin directions, two circles generated two paths (the epicycloid and hypocycloid above), while three circles generated four paths, shown below.
 One great thing about GSP is that you can look at these curves synthetically, where you build them up out of points, lines, and circles, or analytically, where you provide explicit equations for the coordinates of the points that lie on the curves. It turns out that for the family of curves built out of these circles, each having half the radius of the preceding circle, the equations are:
One great thing about GSP is that you can look at these curves synthetically, where you build them up out of points, lines, and circles, or analytically, where you provide explicit equations for the coordinates of the points that lie on the curves. It turns out that for the family of curves built out of these circles, each having half the radius of the preceding circle, the equations are:
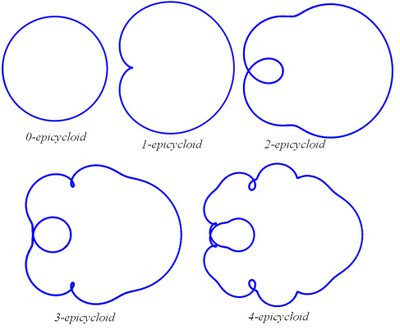
Where we are letting the big circle have radius = 1, n is the number of circles that have been added to the initial base circle, and the coefficients in the expression for y are chosen to be positive or negative to yield different curves (a positive coefficient on the i-th term causes the i-th circle to move counterclockwise, and a negative coefficient causes it to move clockwise). When we choose all positive coefficients and look at n from 0 to 4, we get an interesting evolution of the epicycloid:
If you allow negative coefficients in the y expression and allow allow the circles to spin in different directions, you'll find that the '4th generation' of this family includes some very oddly shaped curves:
Update: The first few generations of these curves are easy to make using Desmos.
See also these related posts:
Scrambler fractal
Brain curve