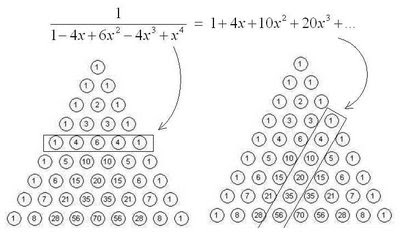
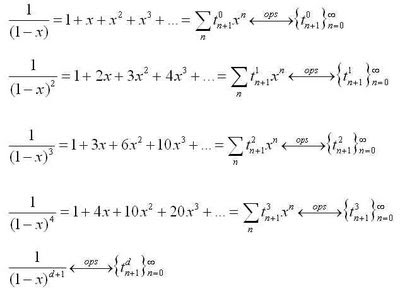The diagram above illustrates a surprising correspondence – if you take the reciprocal of a particular polynomial whose coefficients match the d+1 row of Pascal’s Triangle, you obtain a formal power series whose coefficients are precisely the elements in the dth column of the triangle.The case for the third row is shown above (row and column numbering starts at 0 in Pascal's Triangle), and the case for the fourth row is shown in the diagram below. To actually work out the power series that comes from the reciprocals (well, at least the first few coefficients), the grid method of dividing polynomials works well (I think).
In this way, the rows of the triangle provide all the information required to obtain the columns - a nice correspondence between a finite sequence and an infinite one.
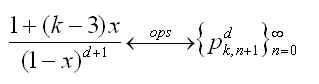
You'll see this correspondence if you spend time investigating the "ordinary power series generating functions" (opsgf's) for the higher dimensional triangular numbers. The row polynomials are just (1-x)^(d+1), while the columns correspond to formal power series whose coefficients are the d-dimensional triangular numbers (see this post). A great place to learn about these opsgf's is H. Wilf's book generatingfunctionology, which can be downloaded here.
You can uncover the general opsgf for higher dimensional triangular numbers by starting with the (1-x)^(-1) rational function, and applying Wilf's 'rule 5' from chapter 2 of generatingfunctionology.
Applying a few other rules, you can obtain an opsgf for the k-polygonal numbers (k = 4 is squares, k = 5 is pentagonals, k = 6 hexagonals, etc.).
