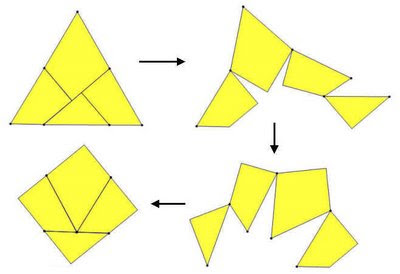
The construction above, which shows how an equilateral triangle can be cut, hinged, and transformed into a square is the very first entry in Hugo Stienhaus's Mathematical Snapshots. Constructing this hinged triangle/square in GSP turns out to be quite a nice activity.Erik Demain's paper Hinged Dissection of Polyominoes and Polyforms takes this example as its starting point, develops the theory of hinged dissections, and shows how this example and others can be taken further.
The references in Demain's paper lead to a great site on geometric dissections (non-hinged), and to the work of Greg N. Frederickson (hinged, non-hinged, and folded dissections).
On Frederickson's site, among many great things, we find a link to a lesson plan that includes instructions on building a physical model of the triangle-square hinged dissection.
