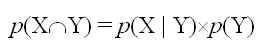There are plenty of probability problems that have counter-intuitive solutions. Problems like these, and how they can undermine common sense, are among the best reasons for looking at probability theory. One set of humbling questions is the family of Monty Hall problems. Another are those related to conditional probability; nice examples of these are problems that involve medical tests that give 'false positive' results.
Simulation is a way of exploring these problems that reveals more than mere theoretical probability calculations do. The structure of the simulation can reflect interesting aspects of the structure of the original problem, and the results reveal a variability that is not apparent when you simply calculate the theoretical probabilities on their own.
This post shows an example of a 'false positive' probability problem and a Fathom simulation for it. This problem was adapted from one found in the 4th edition of Ross's A First Course in Probability (p.75):
A laboratory blood test is 95 percent effective in detecting a certain disease when it is, in fact, present. However, the test also yields a "false positive" result for one percent of healthy persons. (That is, if a healthy person is tested, there is a 0.01 probability that they will test positive for the disease, even though they don't really have it.) If 0.5 percent of the population actually has the disease, what is the probability that a person who has a positive test result actually has the disease?
Here are the attribute definitions that you could use to build a Fathom simulation for this problem:
The attributes are enough to run the simulation, but it is better to also add the following measures:
To run the simulation you can add new cases (try ~500). Using a measures collection, you can re-run this experiment hundreds of times (collecting a 100 measures re-runs the 500 person experiment 100 times).
If you are calculating the theoretical probability by hand, it helps to write down all of the probabilities (fill in the blanks...):
It also helps to visualize the probabilities in a tree diagram:
The outer tips of the tree are filled in using the multiplicative rule for conditional probabilities:
One nice thing about doing this is that you can see how the tree diagram used to calculate the theoretical probabilities is structured in the same way as the "if" statements in the simulation.
A Fathom document implementing this simulation can be found here.