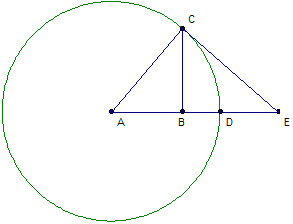
The names of the trigonometric ratios tangent and secant are derived from the Latin “to touch” and “to cut” – the tangent to a figure is a line that touches it in one place, where a secant cuts through it in two or more. But how are these geometric terms related to the ratios that bear their names? The answer can be shown using the diagram at the top of the post - a diagram that used to be a standard one in high school trig text books.
Consider the acute angle BAC. Allow |AC| = 1, and construct a unit circle about A that goes through C. Construct a tangent to this circle at C, and extend the segment AB so that it meets this tangent at E. So, the segment CE lies on the tangent while the segment AE lies on the secant of the unit circle formed around BAC. ACE is a new right triangle that contains the original BAC.
The tangent of BAC is BC/AB (opposite/adjacent), but if we now look at the second triangle ACE, we see tht it is also given by (CE/AC)=(CE/1)=CE - the tangent is measured by the segment of the tangent, CE. Similarly, the secant of BAC is given by AC/AB (hypoteneuse/adjacent), but again turning to the second triangle ACE, we see that this is (AC/AB)=(AE/AC)=(AE/1)=AE - and the secant is provided by the length of the secant, AE.
This treatment was taken from the book "Plane Trigonometry and Tables" by G. Wentworth, published in 1903. In some of the texts of this era, the "primary" trigonometric ratios were sin, sec, and tan (rather than sin, cos, and tan), perhaps owing their primacy to constructions like the one described above.
The cosine was considered a secondary trigonometric ratio - its name coming from the phrase "complement's sine." Along with the usual ratios, texts often presented several convienience ratios that are now antiquated, such as the versedsine vrsin(x) = 1-cos(x) and the half-versed sine or haversine hvrsn(x)= (1/2)vrsin(x).
The most fundamental trigonometric ratio has the most obscure name. It is generally claimed that the word “sine” comes from Latin word for “bend,” but some have suggested that the word is ultimately derived from the name of the curve formed by the gathering of a toga, or from the Latin word for “bowstring.” In Arithmetic, Algebra, Analysis, Felix Klein states that “sine” represents a Latin mis-translation of an Arabic word, but does not go on to explain its origins any further.
My edition of Wentworth is from 1903 - a PDF of the 1887 edition can be downloaded here.
