Thursday, June 2, 2011
sequences on a spiral
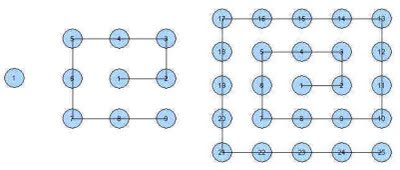
Question 28 of Project Euler has us looking at number spirals. Put the number 1 in the middle of a piece of graph paper and start writing the natural numbers as a square spiral moving outwards from the center. Here is a Tinkerplots file (used to make the pictures in this post) for a spiral with sides length 99 (and a plaintext file, and a smaller a Fathom file). If you begin looking at the spiral, you'll likely find a number of sequences that you can learn more about from the Online Encyclopedia of Integer Sequences.
The numbers on the main upwards diagonal, taken in the order you find them walking on the spiral, are "Hogben's central polygonal numbers," 1, 3, 7, 13, 21, 31, 43, ... (OEIS A002061), although I don't know what makes them polygonal (more on this on a page by Robert Munafo).
If you start summing this diagonal as you walk around, you get a sequence 1, 4, 11, 24, 45, 76, 119, ..., (OEIS A006527) where every number turns out to be the sum of two tetrahedral numbers (a tetrahedral number and one two indexes behind it).
The numbers on the main downwards diagonal (1, 5, 9, 17, 25, 37, 49, 65, ...) provide another sequence that appears in the OEIS as A080335.
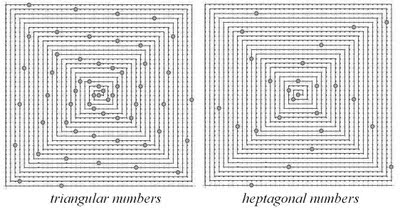
Instead of looking for sequences on the features of the square, you can mark off known sequences on the spiral and see what they look like. I tried this with some polygonal numbers, and found that they (not to surprisingly) form spiral patterns much like they do when plotted on the round number spiral. Below are some pictures of the triangular numbers (OEIS A000217) and the heptagonal numbers (OEIS A000566).
The sequence plot that made this square spiral famous is that of the prime numbers - when you plot the primes on this square spiral you get what is called the Ulam prime spiral. Certain surprising local regularities emerge in parts of the spiral that are best seen if you make it big enough.
What is most noticeable when you plot the primes on the number spiral are the places where primes seem to line up along various diagonals. These clusters indicate the existence of prime-generating quadratics.
Labels:
math,
polygonal,
primes,
project euler,
spirals