star and compound polygons
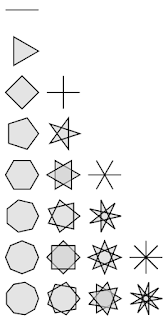
on 2 to 9 vertices
on 2 to 9 vertices
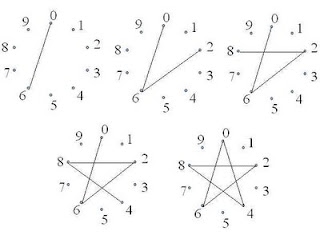
You might draw ten pointed polygons while exploring the multiplication table, for example. In the picture below, skip counting by 6 while drawing a line between the last digits of consecutive numbers gives us a pentagon: counting 0, 6, 12, 18, 24, 30 we draw lines connecting 0, 6, 2, 8, 4, and 0.
skip counting by 6 draws {5/2}
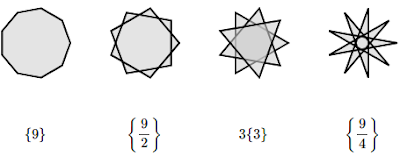
When drawing star and compound polygons by hand, you start with n points spaced evenly around a circle, and then from each point connect to another, always skipping over the same number of points. If you skip over 0 points, you get the regular n-gon. If you skip over k points, and k+1 is relatively prime with n, you will get a star polygon, if n and k+1 share factors, you get a compound of several regular or star polygons.
On 9 points, skipping over 0, 1, 2, and 3
vertices
vertices
It is interesting how an easy to describe algorithm like this, skipping around points on a circle, translates into a program.
The polygons on this page are drawn using some JavaScript (code here), which includes some use of trig functions to place the initial vertices (like points around a unit circle) and modular arithmetic to help traverse the list of points in a circular way. It's a nice example of how math makes its way into how we implement even simple algorithms.
When we go fully over to a mathematical way of expressing how to draw these by using desmos, we can see how mathematics can, in this case, express the algorithm in a surprisingly compact way. You can check out the graph here.
desmos sketch of {7/2},
graph here
graph here
Related links and posts
star polygon page
star polygons in desmos
polygons in the multiplication table