Nineteenth Century Froebelian Doodles
A surprising variety of patterns can be formed by restricting things even further, considering the case where each square is cut in half along a diagonal with half of the square coloured black, the other coloured white (i.e. no blank or completely filled squares, as are found in the images above).
Some arrangements of four Truchet Tiles
Arrangements of these tiles were studied extensively by Sebastien Truchet, whose book on the subject (Method for creating an infinite number of different designs with squares halved into two colours along a diagonal) can be found online here.
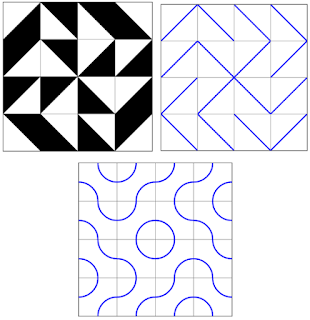
Truchet tiles, as they became known, have been studied extensively and generalised to include other tile sets that are not rotationally symmetrical. In the image below, we start with a traditional Truchet tiling, then only show the diagonals, and finally replacing the diagonals with quarter circles, centred around the vertices where the diagonals used to touch (these tiles, introduced by Cyril Stanley Smith, create interesting patterns of blob-like paths and circles).
Three popular variations on Truchet tiles:
traditional, diagonal, and semi-circles
traditional, diagonal, and semi-circles
To play around with these I've put together a "Truchet Tiles" page here.
There are a number of illustrations in Truchet's text that are worth checking out, and you can reproduce them using the page mentioned above. Here is tiling "38" from Truchet:
tile pattern 38 from Truchet
Here is the same tiling using the Truchet tile page, also rendered using only diagonals and the Smith tiles.
tile pattern 38, generated here
There are lots of questions that can be asked about arrangements of the tiles. Truchet enumerates some of the possible arrangements using symbols and illustrations - below are the first two tables of rows of tiles that he lists (how many will be in the next two tables?).
And replacing the traditional truchet tiles with similarly oriented diagonal and Smith tiles - as you might have noticed, doing this looses information by a factor of 2 for each tile:
Try out the Truchet tile page here: https://dmackinnon1.github.io/truchet/.
Update: More truchet fun in this post.